Más allá del Infinito

Francisco Alfaro
Valeska Canales

2024-12-13

Conjuntos de Números








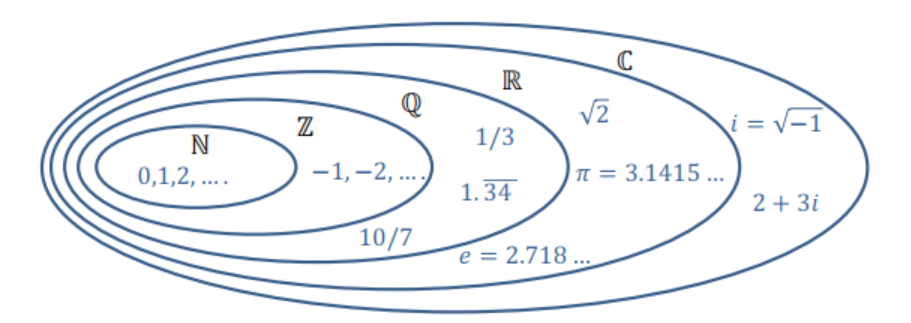
En cantidad de elementos: ¿| \(\mathbb{N}| < |\mathbb{Z}| < |\mathbb{Q}|< |\mathbb{R}|<|\mathbb{C}|\) ?

¿Qué es el infinito?


  • El infinito es algo sin fin.
  • No es un número, sino una idea de continuidad ilimitada.

Historia


Gráficos

Infinito

¿Qué es contar?

Contar es …


N° elementos en un conjunto.

  • Contar personas en una sala.
  • Contar números del 1 al 10.
  • Contar objetos en una canasta.

Fundamento en los Axiomas de Peano

  1. Primer Número: \(0\) o \(1\).
  2. Sucesor: \(1 \rightarrow 2 \rightarrow 3 \rightarrow...\)
  3. Unicidad: Cada número es único.
  4. Inducción: Si un conjunto tiene 0 y sus sucesores, contiene a \(\mathbb{N}\).

Cardinalidad de un Conjunto

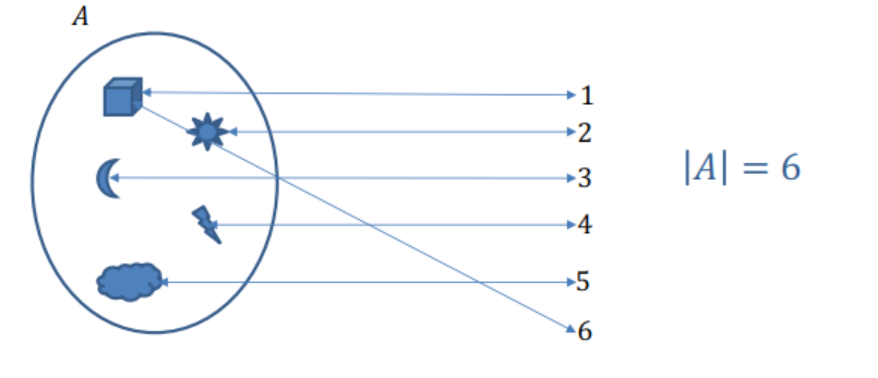
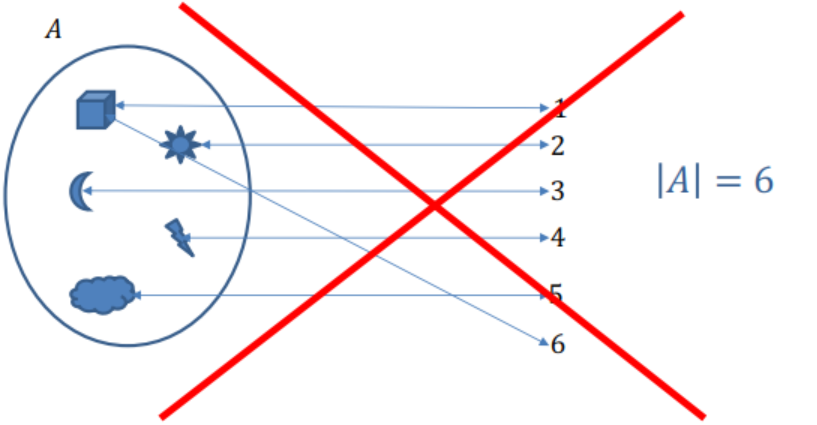
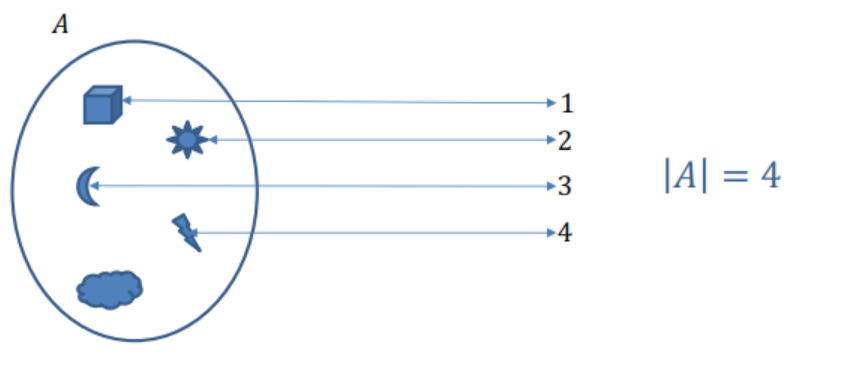
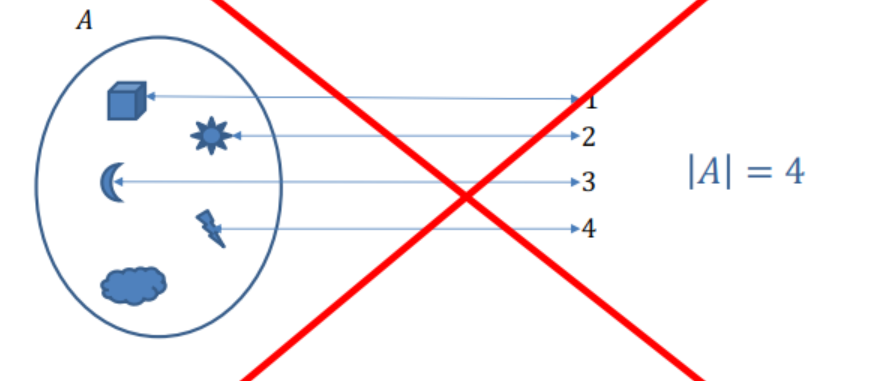
Cardinalidad de un Conjunto

\(|A|\): Contar todos los elementos de \(A\) exactamente una vez.

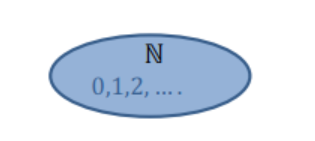
Números Naturales


  • \(\mathbb{N} = \{0,1,2,3,...\}\) son infinitos.
  • También son infinitos:
    • Pares = \(\{2,4,6,...\}\).
    • Impares = \(\{1,3,5,...\}\).
    • Primos = \(\{2,3,5,7,...\}\).

(C) Números Primos son infinitos, Demostración de Euclides.

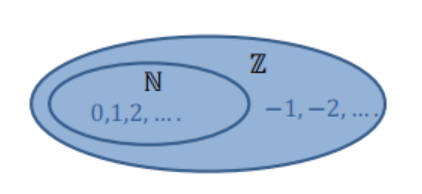
Números Enteros


  • \(\mathbb{N} = \{0,1,2,3,...\}\)
  • \(\mathbb{Z} = \{0,-1,1,-2,2,-3,...\}\)
  • \(\mathbb{N} \subsetneq \mathbb{Z}\) … ¿ \(|\mathbb{N}| < |\mathbb{Z}|\) ?


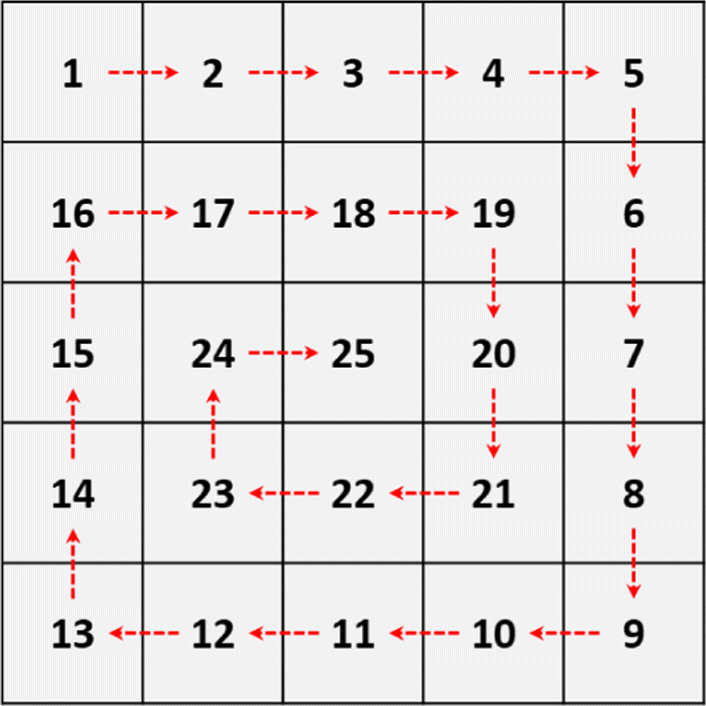
Contemos los números enteros

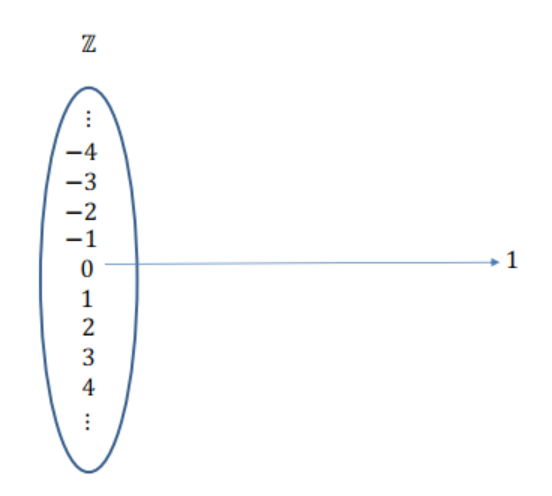
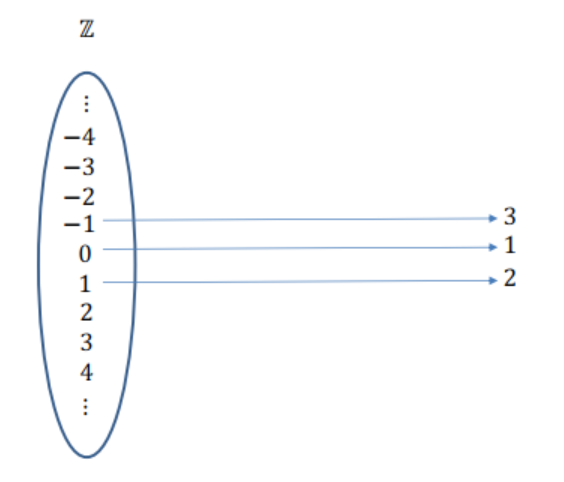
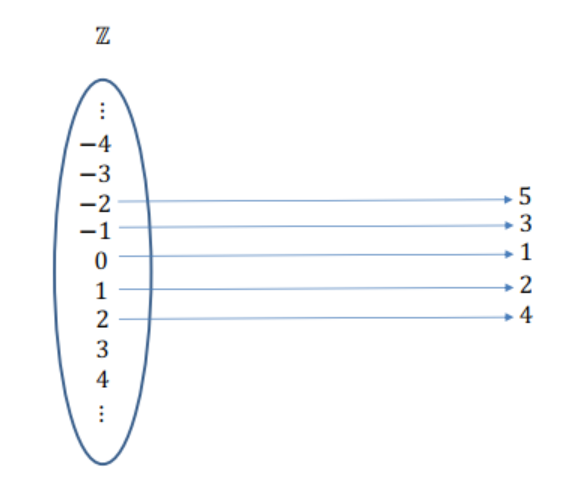
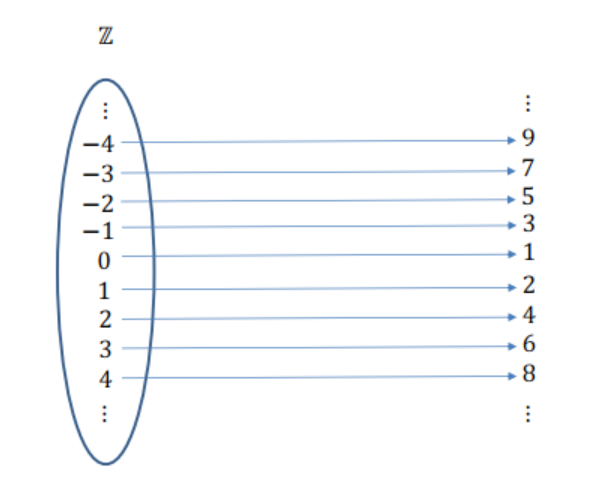
\(\color{black}{\boxed{ |\mathbb{N}| = |\mathbb{Z}| }}\)

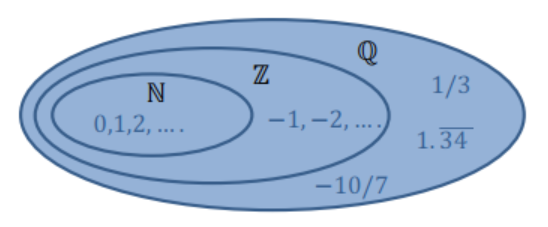
Números Racionales


  • \(\mathbb{Q} = \{ \dfrac{p}{q} | p,q \in \mathbb{Z}, q \neq 0 \}\)
  • \(\mathbb{N} \subsetneq \mathbb{Z} \subsetneq \mathbb{Q}\) … ¿ \(|\mathbb{N}| < |\mathbb{Q}|\) ?


Contemos los números racionales

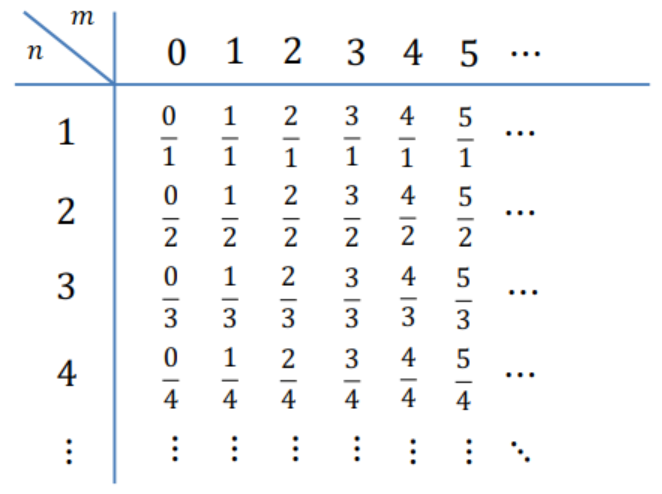
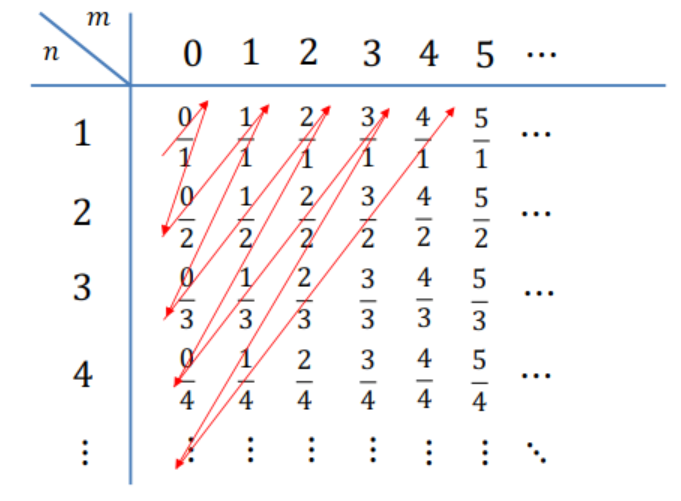
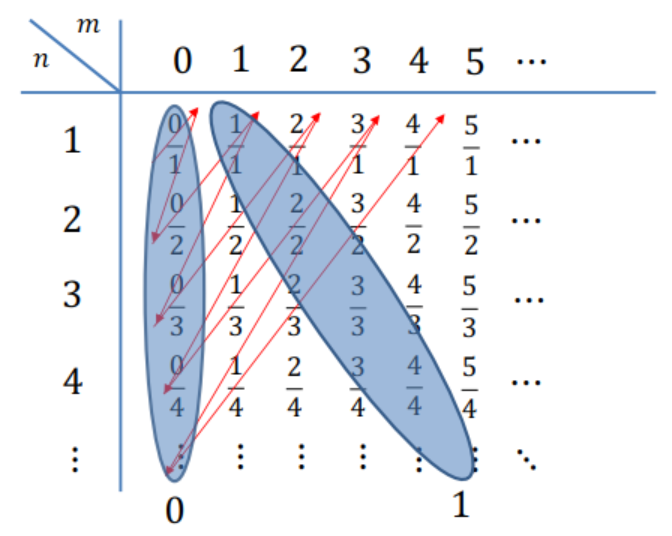
\(\color{black}{\boxed{ |\mathbb{N}| \leq |\mathbb{Q_{+}}| \leq |\mathbb{N}| }}\)

\(\color{black}{\boxed{ |\mathbb{N}| = |\mathbb{Z}| = |\mathbb{Q}| }}\)

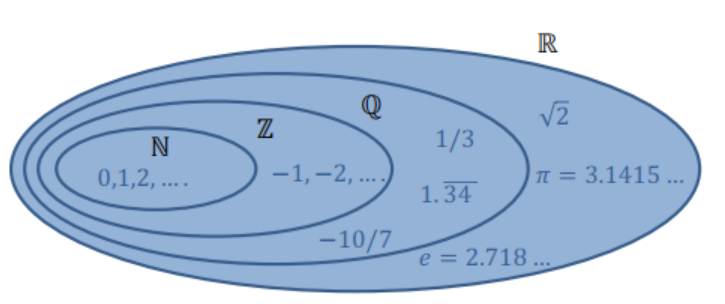
Números Reales


  • \(\mathbb{R} = \{ \sqrt{2}, \pi, \mathrm{e}, ... \}\)
  • ¿ \(|\mathbb{N}| < |\mathbb{R}|\) ?


Números Reales


En 1891, Cantor probó que es imposible enumerar todos los números reales en \((0,1)\).


\(\color{black}{\boxed{\aleph_1 = |\mathbb{R}| > |\mathbb{N}| = |\mathbb{Z}| = |\mathbb{Q}| = \aleph_0}}\)

Infinito

Hotel de Hilbert

El Hotel de Hilbert


  1. Hotel infinito: Siempre hay espacio para más.
  2. Truco: Mueve cada huésped adelante.
  3. Lección: El infinito desafía la intuición.

🐶 Bienvenidos al Hotel de Vale


Un lugar mágico con infinitas habitaciones para perritos, donde cada uno tiene su espacio y siempre son bienvenidos.

✨ !Siempre hay espacio para uno más!

Caso 1: Llega un Nuevo Perrito

  • El hotel está completo, cada habitación tiene un perrito.
  • Llega un Nuevo Perrito … ¿Qué hacemos?

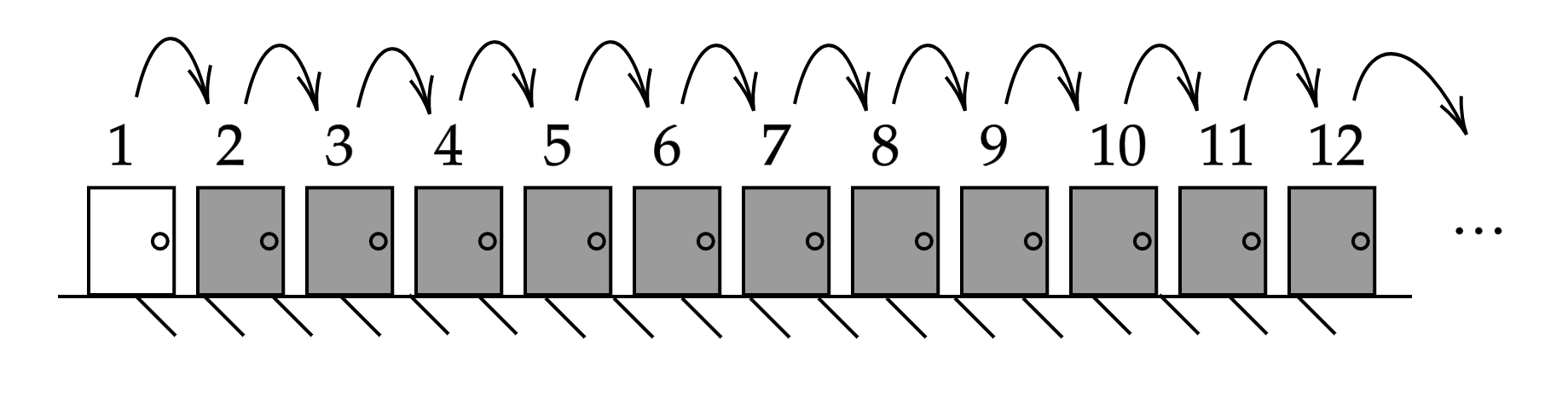
Caso 2: Infinitos Perritos

  • El hotel está completo, cada habitación tiene un perrito.
  • Llega un bus con infinitos perritos … ¿Qué hacemos?

Caso 3: Infinitos Buses y Perritos

  • El hotel está completo, cada habitación tiene un perrito.
  • Llegan inifinitos buses con infinitos perritos … ¿Qué hacemos?

Caso 3: Infinitos Buses y Perritos

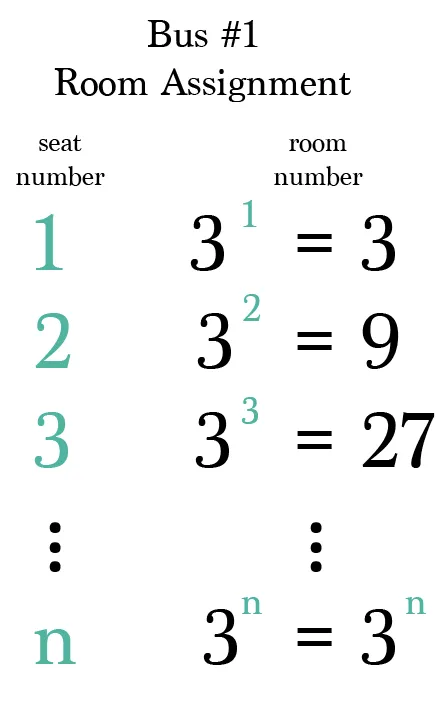
Conclusiones


  • 🌌 El \(\infty\): Conceptos que desafían la intuición.
  • 📏 Cardinalidad: Diferentes tamaños de infinito.
  • 🐶 Hotel de Perritos: Infinito de forma entretenida.

🎉 ¡Gracias por Participar!


❓¿Preguntas?

👏 Responder encuesta

🥳 Gracias de Nuevo

🔗 Nuestro Sitio Web: seth-nut.github.io/resources.